photo credit Camera Obscura Vondelpark, Amsterdam by Stef Nagel
Camera is one of the main object in computer vision. Understanding how a camera works can actually get us to many interesting problems of computer vision such as image panorama or 3D reconstruction.
Pinhole camera model
Camera functioning simulates the way human eyes work. Yet, despite the incredibe complexity of the eyes (the second-most, only after the brain), or how insane modern cameras could get to nowaday, the underlining mechanism of cameras, and especially ones employed in most computer vision problems, is somewhat simpler, a pinhole camera model which is shown in Figure 1.
We see things because there are light rays reflecting from them come into our eyes. The colors we perceive are the wavelengths that are not absored from the objects’ surfaces. To captured images, we use photographic films, thin plastic sheets coasted with light-sensitive substances, that react to light rays contact (read more at wiki).
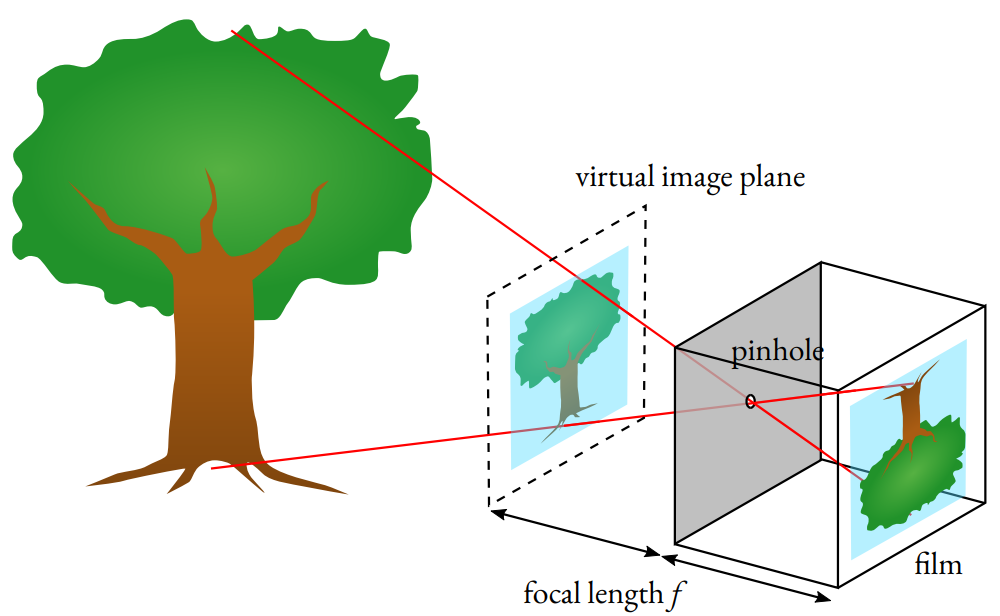
If we simply put a film in front of an object, we get blurry images, because light rays reflecting from every part of the object end up at the same position on the film, and it is screwed up. Thus, to limit the number of rays that can touch the film, we put a barrier with a pinhole (or aperture) on it. Hence, up to a certain point the smaller the hole is, the sharper but dimmer the image becomes (read more on how to select pinhole size). Light rays reflecting from an object pass through and create an inverted image on the film. That basically makes a (pinhole) camera, and the effect is called camera obscura effect.
A pinhole camera creates real image on the film, hence the film is usually known to as real image plane. To ease out the mathematic that involves in explaining the model, we consider a virtual image plane that is symmetric to the real plane about the center of projection (the aperture).
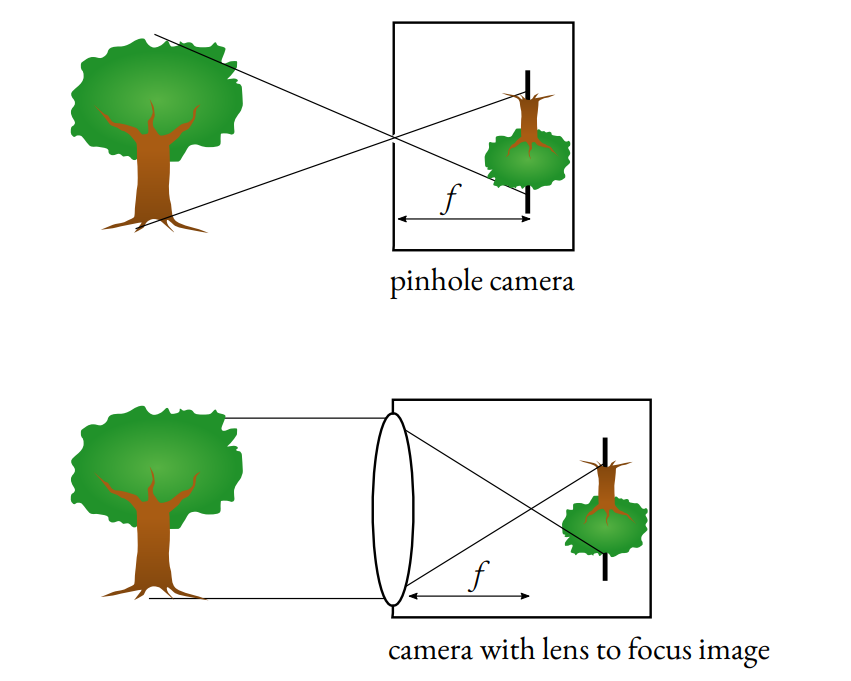
In pinhole camera model, the focal length is defined to be the distance from the center of projection to the image plane. This is, however, different from the focal length of a lens (usually used in lens cameras), which is the distance to the plane where incoming parallel rays meet. Because of having no lens, if we consider the same definition for a pinhole camera, its focal length would be infinity.
As most of commodity cameras employed in research compose are based on similar structure with thin lenses, small apertures and light sensors in place of films, the pinhole camera model is usually employed in explaining and modelling image formation in computer graphic and computer vision research.
Image formation
The camera model gives us the relationship between the location of a pixel in 2D image and their corresponding points in the real 3D space. In this section, we are to find the formulas that convert image pixels to 3D point cloud, and vice versa.
Pixel locations are specified by their coordinates in a 2D image, whereas point clouds are situated in 3D space with a different coordination system. To associate one with the other, we need an intermediate, i.e. the camera space.
Before going into the image formation details, we are to describe the coordinate systems that would involve in the process
Image coordinate system is the coordinate system that attachs to each image, which is used to specify pixel location. Conventionally, from viewers’ perspective, the the origin is at top-left corner of the image with \(x\)-axis pointing rightward, and \(y\)-axis downward.
Camera coordinate system has its origin attach to the camera. Computer vision convention uses right-handed system with \(z\)-axis pointing toward the object at which the camera is looking (hence going outward of the camera and inward the image plane), while \(y\)-axis pointing downward, and \(x\)-axis rightward. Note that this convention used by OpenCV and may be different from the view coordinate system employed in computer graphics softwares (such as Blender) which have the camera looking at the negative z-coordinates and \(y\)-axis pointing upward.
World coordinate system relates a camera to other objects in a scene.

Let \( \text{P} = {\begin{bmatrix} X & Y & Z \end{bmatrix}}^T \) be an arbitrary 3D point seen by a camera situating at the origin \( \text{O} \) of its camera space \( \text{O}XYZ \), and \( \mathbf{p} = {\begin{bmatrix} u & v \end{bmatrix}}^T \) be the image of \(\text{P}\), expressed in the image coordinate system \( \mathbf{o}uv \). The point \( \bf p \) represents a pixel in an image captured by the camera, which is formed by intersecting the light ray from \( \text{P} \) passing through the camera optical center \( \rm O \) and the image plane.
Assuming that the projective plane is perpendicular to the \(Z\)-axis of the camera coordinate system; the intersection is at the principal point \( \text{F} = {\begin{bmatrix} 0 & 0 & f \end{bmatrix}}^T \), which is expressed in the image coordinate system as \( \bf c = {\begin{bmatrix} c_x & c_y \end{bmatrix}}^T \). Let \( \mathbf{c}xy \) be the coordinate system at \( \bf c \), with 2 axes parallel to the 2 image axes. The relationship between \( \mathbf{o}uv \) and \( \mathbf{c}xy \) is given by
\[ u = x + c_x \qquad \text{and} \qquad v = y + c_y, \qquad (1) \]
Noted that the quantities in Equation \(1\) are all expressed in image unit, or pixels. To convert to real world measurement we need the imager elements \( s_u, s_v \) that count the number of pixels per real world unit (usually inch, hence the names dots per inch (DPI) or pixels per inch (PPI)).
The projected object size relating to the object’s real size is parameterized by the distance between the projective plane and the camera center, i.e. \( f \), the focal length. Similar triangles give:
\[ x = s_u\dfrac{fX}{Z} \qquad \text{and} \qquad y = s_v\dfrac{fY}{Z}, \] thus \[ u = s_u\dfrac{fX}{Z} + c_x \qquad \text{and} \qquad v = s_v\dfrac{fY}{Z} + c_y \qquad(2) \]
Since \( \bf p \) is in a 2D projective space (an image plane), it could be represented by a 3-component vector \( \tilde{\bf p} = {\begin{bmatrix} u & v & w \end{bmatrix}} ^T \) using homogeneous coordinate, turning Equation \(2\) into
\[ \begin{bmatrix} u \\ v \\ w \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \end{bmatrix} \quad \text{or} \quad\tilde{\bf p}=\mathbf{K}\text{P}, \qquad(3) \]
where \(f_x = s_uf\), and \(f_y = s_vf\). To retrieve the Cartesian value of \(u,v\) from the homogeneous coordinates, we need to scale the results of Equation \(3\) such that \(w=1\), i.e. divided by \(Z\).
Noted again that the matrix \( \bf {K} \) contains all the camera internal parameters (in pixel unit), such as the focal length \( f_x, f_y \) and principal point coordinate \( c_x, c_y \), thus is called the camera intrinsic matrix.
Application: reconstructing partial point cloud from depth images
So far, we have found the relationship between a 3D point in the camera coordinate and its image in the image space. Equation (2) and (3) derive the 2D image coordinates given 3D coordinates in the camera space.
The reverse direction, retrieving 3D coordinates of a point for each image pixel is ill-posed. Remember that the third dimension of the points have been squashed during projection. Thus, to recover the 3D coordinates, it is necessary to have corresponding depth or \(Z\) coordinate of each pixels.
Depth cameras, either commodity like the Kinect or more sophisticated like laser scaners, provide at each pixel the distance from the camera to the corresponding objects.
Equation \(2\) shows how image coordinates can be obtained from 3D real world coordinate point \(P\). To reconstruct the 3D point cloud from a given image, we take its inverse:
\[ X = \dfrac{(u-c_x)Z}{f_x} \quad\text{and}\quad Y = \dfrac{(v-c_y)Z}{f_y},\qquad (4) \]
Structured light devices like Kinect or RealSense devices, output directly the \(Z\) coordinates of real-world points in the camera coordinate system, thus, the equations are well provided. Plugging in the provided \(Z\) and we are good to go.
In other cases where pure depth or point distance is provided (i.e. \(\rm OP\) instead of \(\rm OP’\) in Figure \(2\)), we need to take extra steps to compute \(Z\). Similar triangles give:
\[ \dfrac{\rm OP’}{\rm OF} = \dfrac{\rm OP}{\rm O\bf p} \Leftrightarrow \dfrac{Z}{f} = \dfrac{d}{\sqrt{f^2 + m^2}}, \]
where the size \( m \) of the projection \(F\bf p\) relating to the size \( n \) of the real segment \( \text{PP’} \) is given by similar triangles:
\[ \dfrac{F\bf p}{PP’} = \dfrac{\rm OF}{\rm OP’} \Leftrightarrow \dfrac{m}{n} = \dfrac{f}{Z}, \]
Hence,
\[ Z = \dfrac{df}{\sqrt{f^2 + \dfrac{f^2n^2}{Z^2}}} = \dfrac{d}{\sqrt{1 + \dfrac{X^2 + Y^2}{Z^2}}}, \qquad(5) \]
Equation \(4\) gives \[ \dfrac{X}{Z} = \dfrac{u-c_x}{f_x},\quad\text{and}\quad \dfrac{Y}{Z} = \dfrac{v-c_y}{f_y},\qquad (6) \]
Substituting Equation \(6\) into \(5\) gives:
\[ Z = \dfrac{d}{\sqrt{\left(\dfrac{u-c_x}{f_x}\right)^2 + \left(\dfrac{v-c_y}{f_y}\right)^2 + 1}} \]
In general, from an image pixel at \((u,v)\) and camera instrinsic parameters, the 3D coordinates \((X, Y, Z)\) can be computed by \[ A = \dfrac{u-c_x}{f_x}, \qquad B = \dfrac{v-c_y}{f_y}, \\ X = A \times Z, \qquad Y = B \times Z, \
\]
where \(Z\) is either given directly by depth sensors or computed by \[ Z = \dfrac{d}{\sqrt{ A^2 + B^2 + 1}}, \]
where \(d\) is the distance from object points to the camera.
The process can obtain for each depth-available pixel in an image the corresponding 3D coordinates. The set of 3D points, together with their color as provided by the optical image, is the partial point cloud of the object or scene. The point cloud is partial because only those visible point to the camera, both optical and depth, are included.